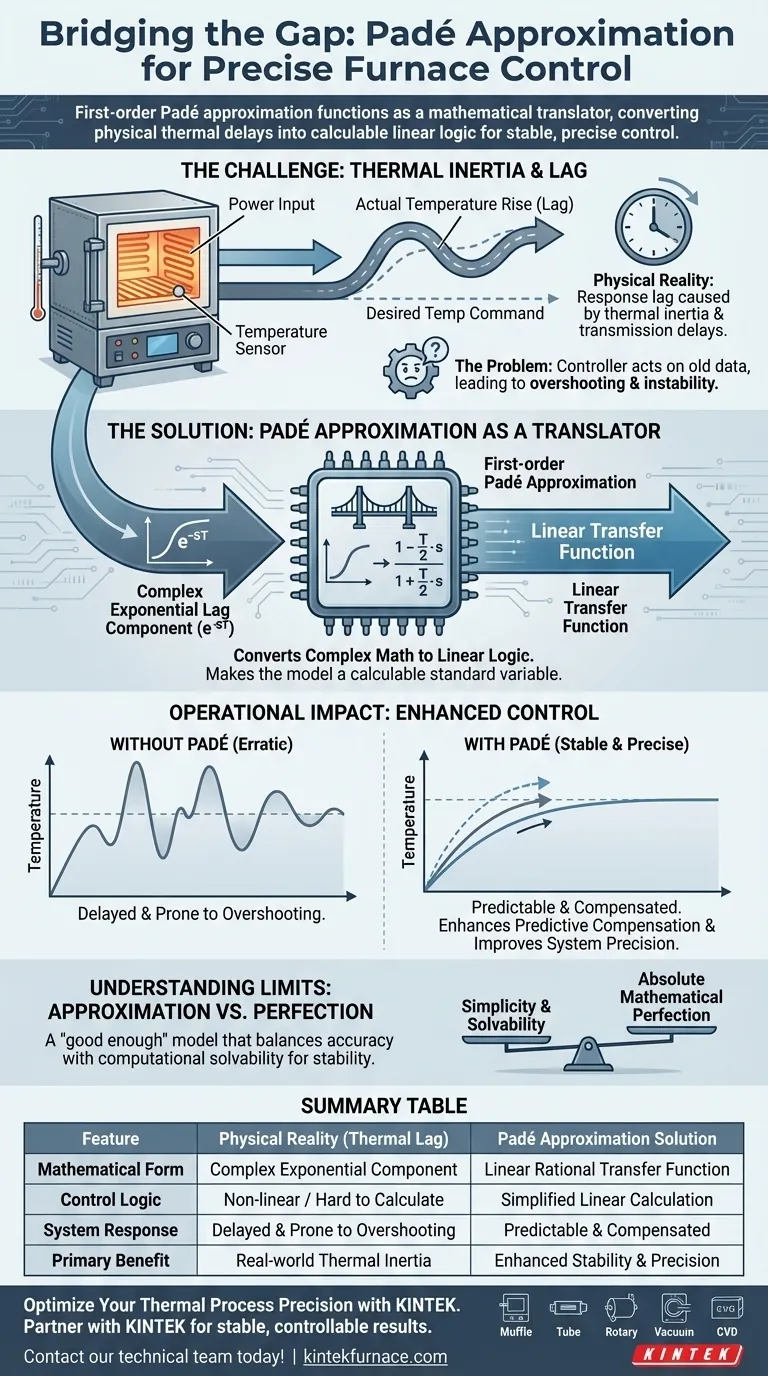
一阶 Pade 近似充当数学翻译器,弥合物理热延迟与控制系统逻辑之间的差距。它通过将由热惯性和传输延迟引起的复杂指数滞后分量转换为可计算的线性传递函数来解决电炉调节中的技术挑战。这种转换使控制器能够有效补偿响应滞后,确保系统保持稳定和精确。
工业电炉具有显著的热惯性,会产生标准算法难以管理的延迟。一阶 Pade 近似将这些复杂的延迟简化为线性格式,使控制系统能够可靠地预测行为并保持精确的温度调节。
挑战:热惯性和滞后
电炉的物理现实
在工业环境中,电炉不会立即响应功率变化。响应滞后始终存在,由热惯性和传输延迟引起。
时间延迟的问题
当控制器发出提高加热的信号时,实际温度上升会稍后发生。这种传输延迟会在命令和结果之间产生脱节。
如果没有适当的建模,控制器将对旧数据做出反应。这通常会导致目标温度过冲或系统不稳定。

Pade 近似如何解决问题
将复杂数学转换为线性逻辑
在数学上,纯时间延迟表示为复杂的指数滞后分量。这些很难直接用于标准的线性控制回路计算。
一阶 Pade 近似通过将指数项转换为线性传递函数来解决此问题。它创建了一个有理分数来近似延迟。
使模型可计算
转换后,延迟成为系统方程中可管理的一部分。控制算法现在可以将滞后作为标准变量进行处理,而不是复杂的异常。
对温度控制的操作影响
增强预测性补偿
通过线性化延迟,电炉控制器可以更可靠地预测温度随时间的反应。它可以“看到”即将到来的延迟,并及早调整功率输出来进行补偿。
提高系统精度和稳定性
最终结果是一个更强大的系统。由于控制器能够准确地考虑热惯性,因此可以防止出现剧烈波动。
这可以提高实际运行中的精度和稳定性,确保电炉在没有持续振荡的情况下保持正确的温度。
理解近似的局限性
近似与完美
重要的是要记住,这种方法是一种近似,而不是物理延迟的精确复制。它将指数函数的无限级数简化为有限的线性比率。
平衡简单性和准确性
虽然对于稳定标准电炉回路非常有效,但它以计算可解性为代价来换取绝对的数学完美。它提供了一个“足够好”的模型来确保稳定性,而无需过多的处理能力。
为您的控制策略做出正确选择
在设计或调整电炉的温度控制模型时,请考虑此近似值与您的特定目标如何对齐。
- 如果您的主要重点是系统稳定性:使用 Pade 近似来防止由加热元件和传感器之间的延迟引起的振荡。
- 如果您的主要重点是算法的简单性:实施此方法将复杂的非线性延迟数学转换为易于计算的标准线性函数。
通过将物理滞后转换为线性数学值,您可以将混乱的热响应转化为可预测、可控的过程。
摘要表:
| 特征 | 物理现实(热滞后) | Pade 近似解决方案 |
|---|---|---|
| 数学形式 | 复杂指数分量 | 线性有理传递函数 |
| 控制逻辑 | 非线性/难以计算 | 简化的线性计算 |
| 系统响应 | 延迟且易于过冲 | 可预测且已补偿 |
| 主要优点 | 实际热惯性 | 提高稳定性和精度 |
通过 KINTEK 优化您的热工艺精度
克服热惯性需要数学精度和高性能硬件。KINTEK 提供行业领先的加热解决方案,并得到专家研发和制造的支持。无论您需要马弗炉、管式炉、旋转炉、真空炉还是 CVD 系统,我们的实验室高温炉均可完全定制,以满足您独特的热调节需求。
不要让响应滞后损害您的结果。与 KINTEK 合作,实现您的研究所需的稳定性和控制。 立即联系我们的技术团队,讨论您的定制炉需求!
图解指南
参考文献
- Serdar Ekinci, Євген Зайцев. Efficient control strategy for electric furnace temperature regulation using quadratic interpolation optimization. DOI: 10.1038/s41598-024-84085-w
本文还参考了以下技术资料 Kintek Furnace 知识库 .



















